Rekursion

Man kann Prozeduren auch sich selber wieder aufrufen lassen - dies nennt sich Rekursion. Dabei ist nat"urlich darauf zu achten, dass dies nicht unendlich oft geschieht, sondern auch irgendwann endet.

Beispiel: Es soll das Kapital berechnet werden, wenn ein Anfangskapital mehrere Jahre bei gleichem Zinssatz verzinst wird.

to zinseszins :k :n :p
  ifelse (:n > 0) [
    output zinseszins (:k*(1+:p)) (:n-1) :p
   ] [
    output :k
   ]
end

Damit kann nun bei einem Kapital von berechnet werden, was man nach Jahren bei hat:

? print zinseszins 100 10 0.05
162.889462677744

Aufgabe 8.1   Schreibe eine Prozedur zinseszinsgewinn, die den Gewinn bei einer derartigen Geldanlage berechnet!

Aufgabe 8.2   Schreibe eine Prozedur potenz, die durch Rekursion die Potenz f"ur eine nat"urliche Zahl berechnet!

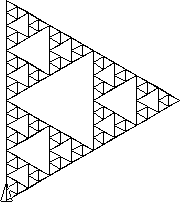
Beispiel: Sierpinski-Dreieck
Unter dem Sierpinski-Dreieck versteht man eine Figur, die dadurch entsteht, dass man

• ein gleichseitiges Dreieck nimmt,
• die Seitenl"ange halbiert
• und damit neue Dreiecke in alle Ecken zeichnet.

Dieser Proze"s wird dann beliebig oft wiederholt. Da wir das nicht unendlich oft machen k"onnen, m"ussen wir irgendwann abbrechen - beispielsweise sobald die Seitenl"ange zu klein wird.

to sierpinski :s
  ifelse (:s > 20) [
    repeat 3 [sierpinski (:s/2) fd :s*2 rt 120]
   ] [
    repeat 3 [repeat 3 [fd :s rt 120] fd :s*2 rt 120]
   ]
end

Der Aufruf sierpinski 100 liefert folgendes Bild:

Aufgabe 8.3   Schreibe eine Prozedur koch, die die Koch-Kurve zeichnet!

Die Koch-Kurve entsteht aus einer Strecke indem man das mittlere Drittel der Strecke entfernt und stattdessen ein gleichseitiges Dreieck an gleiche Stelle zeichnet. Nun wiederholt man diesen Vorgang f"ur jede Teilstrecke.

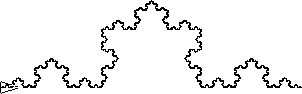
Aufgabe 8.4   Schreibe eine Prozedur kochflocke, die Koch-Kurven so zusammensetzt, dass eine Schneeflocke erkennbar wird.

Man kann auf sehr einfache Weise durch Rekursion Muster erzeugen:

to spirale :s :w
  fd :s
  rt :w
  spirale :s (:w+10)
end

Beispiele:

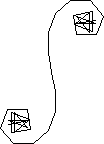
spirale 20 20

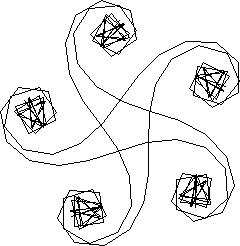
spirale 30 1

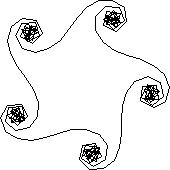
spirale 14 3